Linear regression with a two-level factor explanatory variable

Last updated on 2024-03-12 | Edit this page

Estimated time: 40 minutes

Overview

Questions

  • How can we explore the relationship between one continuous variable and one categorical variable with two groups prior to fitting a simple linear regression?
  • How can we fit a simple linear regression model with one two-level categorical explanatory variable in R?
  • How does the use of the simple linear regression equation differ between the continuous and categorical explanatory variable cases?
  • How can the parameters of this model be interpreted in R?
  • How can this model be visualised in R?

Objectives

  • Use the ggplot2 package to explore the relationship between a continuous variable and a two-level factor variable.
  • Use the lm command to fit a simple linear regression with a two-level factor explanatory variable.
  • Distinguish between the baseline and contrast levels of the categorical variable.
  • Use the jtools package to interpret the model output.
  • Use the jtools and ggplot2 packages to visualise the resulting model.

In this episode we will study linear regression with one two-level categorical variable. We can explore the relationship between two variables ahead of fitting a model using the ggplot2 package.

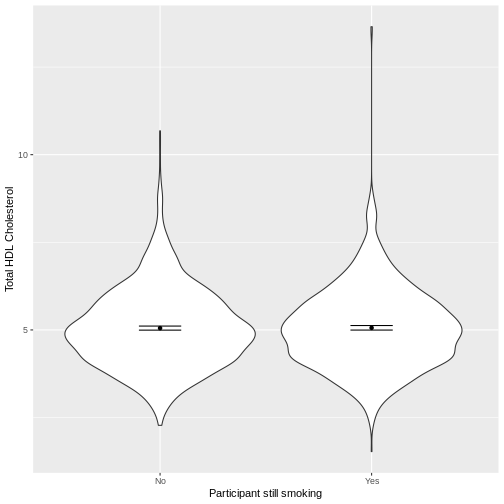
Exploring the relationship between a continuous variable and a two-level categorical variable

Let us take SmokeNow and TotChol as an example. SmokeNow describes whether someone who has smoked > 100 cigarettes in their life is currently smoking. TotChol describes the total HDL cholesterol in someone’s blood. In the code below, we first remove rows with missing values using drop_na() from the tidyr package. We then initiate a plotting object using ggplot. We select the variables of interest inside aes(). We then make a violin plot using geom_violin. The shapes of the objects are representative of the distributions of TotChol in the two groups. We overlay the means and their 95% confidence intervals using stat_summary(). Finally, we change the axis labels using xlab() and ylab().

R 

dat %>%
  drop_na(c(SmokeNow, TotChol)) %>%
  ggplot(aes(x = SmokeNow, y = TotChol)) +
  geom_violin() +
  stat_summary(fun = "mean", size = 0.2) +
  stat_summary(fun.data = "mean_cl_normal", geom = "errorbar", width = 0.2) + 
  xlab("Participant still smoking") +
  ylab("Total HDL Cholesterol")

Notes on thefunandfun.dataarguments instat_summary()

The fun and fun.data arguments both apply statistical operations to data but do slightly different things. fun takes data as vectors and will return single values for each these vectors. In the above example, we calculate the mean for each vector (each SmokeNow group). fun.data expects a dataset (which may be a simple vector) and provides three values for each dataset: y, ymin and ymax. In our case, ymin is lower bound of the confidence interval and ymax is the upper bound of the confidence interval.

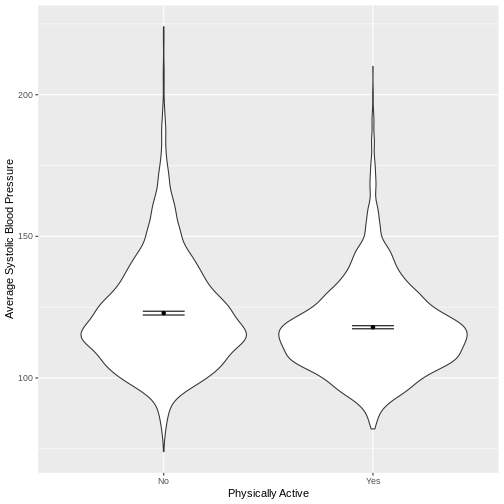
Exercise

You have been asked to model the relationship between average systolic blood pressure and physical activity in the NHANES data. Use the ggplot2 package to create an exploratory plot, ensuring that it includes the following elements:

  1. Average systolic blood pressure (BPSysAve) on the y-axis and physical activity (PhysActive) on the x-axis, from the NHANES data.
  2. These data presented using a violin plot.
  3. The y-axis labelled as “Average Systolic Blood Pressure” and the x-axis labelled as “Physically Active”.

R 

dat %>%
  drop_na(c(PhysActive, BPSysAve)) %>%
  ggplot(aes(x = PhysActive, y = BPSysAve)) +
  geom_violin() +
  stat_summary(fun = "mean", size = 0.2) +
  stat_summary(fun.data = "mean_cl_normal", geom = "errorbar", width = 0.2) +
  xlab("Physically Active") +
  ylab("Average Systolic Blood Pressure")

Fitting and interpreting a simple linear regression model with one two-level categorical variable

We proceed to fit a linear regression model using the lm() command, as we did in the previous episode. The model is then interpreted using summ().

Note that even though we are using the same equation of the simple linear regression model (\(E(y) = \beta_0 + \beta_1 \times x_1\)), our interpretation of the summ() output differs slightly from our interpretation in the previous episode. Recall that our categorical explanatory variable has two levels, "No" and "Yes". One of these is taken by the model as the baseline ("No"), the other as the contrast ("Yes"). The first level alphabetically is chosen by R as the baseline, unless specified otherwise.

The intercept in the summ() output is the estimated mean for the baseline, i.e. for participants that stopped smoking. The SmokeNowYes estimate is the estimated average difference in TotChol between participants that stopped smoking and participants that did not stop smoking. We can therefore write the equation for this model as:

\[E(\\text{Total HDL cholesterol}) = 5.053 + 0.008 \\times x\_1\],

where \(x_1 = 1\) if a participant has continued to smoke and 0 otherwise (i.e. the participant stopped smoking).

R 

TotChol_SmokeNow_lm <- dat %>%
  lm(formula = TotChol ~ SmokeNow)

summ(TotChol_SmokeNow_lm, confint = TRUE, digits = 3)

OUTPUT 

MODEL INFO:
Observations: 2741 (7259 missing obs. deleted)
Dependent Variable: TotChol
Type: OLS linear regression 

MODEL FIT:
F(1,2739) = 0.031, p = 0.861
R² = 0.000
Adj. R² = -0.000 

Standard errors: OLS
------------------------------------------------------------
                     Est.     2.5%   97.5%    t val.       p
----------------- ------- -------- ------- --------- -------
(Intercept)         5.053    4.995   5.111   170.707   0.000
SmokeNowYes         0.008   -0.078   0.094     0.175   0.861
------------------------------------------------------------

Exercise

  1. Using the lm() command, fit a simple linear regression of average systolic blood pressure (BPSysAve)
    as a function of physical activity (PhysActive). Name this lm object BPSysAve_PhysActive_lm.
  2. Using the summ() function from the jtools package, answer the following questions:
  1. What average systolic blood pressure does the model predict, on average, for an individual who is not physically active?
  2. By how much is average systolic blood pressure expected to change, on average, for a physically active individual?
  3. Given these two values and the names of the response and explanatory variables, how can the general equation \(E(y) = \beta_0 + {\beta}_1 \times x_1\) be adapted to represent this model?

R 

BPSysAve_PhysActive_lm <- dat %>% 
  lm(formula = BPSysAve ~ PhysActive)

summ(BPSysAve_PhysActive_lm, confint = TRUE, digits = 3)

OUTPUT 

MODEL INFO:
Observations: 6781 (3219 missing obs. deleted)
Dependent Variable: BPSysAve
Type: OLS linear regression 

MODEL FIT:
F(1,6779) = 133.611, p = 0.000
R² = 0.019
Adj. R² = 0.019 

Standard errors: OLS
-------------------------------------------------------------------
                         Est.      2.5%     97.5%    t val.       p
------------------- --------- --------- --------- --------- -------
(Intercept)           122.892   122.275   123.509   390.285   0.000
PhysActiveYes          -5.002    -5.851    -4.154   -11.559   0.000
-------------------------------------------------------------------
  1. 122.892 mmHg
  2. Decrease by 5.002 mmHg
  3. \(E(\text{BPSysAve}) = 122.892 - 5.002 \times x_1\), where \(x_1 = 0\) if an individual is not physically active and \(x_1 = 1\) if an individual is physically active.

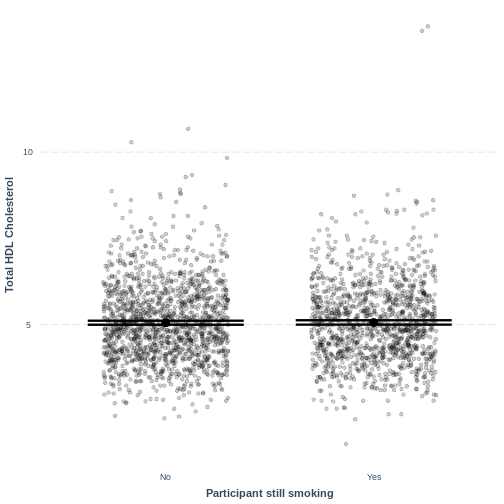
Visualising a simple linear regression model with one two-level categorical explanatory variable

Finally, we visually inspect the parameter estimates provided by our model. Again we can use effect_plot() from the jtools package. We include jitter = c(0.3, 0) and point.alpha = 0.2 so that points are spread out HORIZONTALLY and so that multiple overlayed points create a darker colour, respectively. The resulting plot differs from the scatterplot obtained in the previous episode. Here, the plot shows the mean Total HDL Cholesterol estimates for each level of SmokeNow, with their 95% confidence intervals. This allows us to see how different the means are predicted to be and within what range we can expect the true population means to fall.

R 

effect_plot(TotChol_SmokeNow_lm, pred = SmokeNow,
            plot.points = TRUE, jitter = c(0.3, 0), point.alpha = 0.2) +
  xlab("Participant still smoking") +
  ylab("Total HDL Cholesterol")

Notes onjitterandpoint.alpha

Including jitter = c(0.3, 0) results in points being randomly jittered horizontally. Therefore, your plot will differ slightly from the one shown above. Re-running the code will also give a slightly different jitter. If you would want to fix the jitter to one randomisation, you could run a set.seed() command ahead of effect_plot. set.seed() takes one positive value, which specifies the randomisation. This can be any positive value. For example, if you run the code below, your jitter will match the one shown on this page:

R 

set.seed(20) #fix the jitter to a particular pattern
effect_plot(TotChol_SmokeNow_lm, pred = SmokeNow,
            plot.points = TRUE, jitter = c(0.3, 0), point.alpha = 0.2) +
  xlab("Participant still smoking") +
  ylab("Total HDL Cholesterol")

Including point.alpha = 0.2 introduces opacity into the plotted points. As a result, if many points are plotted on top of each other, this area shows up with darker dots. Including opacity allows us to see where many of the points lie, which is handy with big public health data sets.

Exercise

Use the jtools package to visualise the model of BPSysAve as a function of PhysActive.
Ensure that the x-axis is labelled as “Physically active” and the y-axis is labelled as “Average Systolic Blood Pressure”. How does this plot relate to the output given by summ?

R 

effect_plot(BPSysAve_PhysActive_lm, pred = PhysActive,
plot.points = TRUE, jitter = c(0.3, 0), point.alpha = 0.2) +
  xlab("Physically Active") +
  ylab("Average Systolic Blood Pressure")

This plot shows the mean estimates for BPSysAve for the two groups, alongside their 95% confidence intervals. The mean estimates are represented by the Intercept for the non-physically active group and by Intercept + PhysActiveYes for the physically active group.

Key Points

  • As a first exploration of the data, construct a violin plot describing the relationship between the two variables.
  • Use lm() to fit a simple linear regression model.
  • Use summ() to obtain parameter estimates for the model.
  • The intercept estimates the mean in the outcome variable for the baseline group. The other parameter estimates the difference in the means in the outcome variable between the baseline and contrast group.
  • Use effect_plot() to visualise the estimated means per group along with their 95% CIs.